Ions and Cell Membranes
1.3.1 - Ions and Cell Membranes
This video is a good place to start for understanding membrane potentials.
Electrophysiology, by definition, is the study of the electrical properties of biological cells. It involves measurements of electric current and electrical activity of neurons and other cells. The plasma membranes of most living cells are electrically polarized. The cell membrane has the ability to separate charges by performing work; the charges do not result from the separation of electrons (like metal wire) but rather the separation of charged ions. This separation occurs through the action of the Na-K ATPase pump.
Two very important terms to remember when dealing with the electrical properties of cells are the resting membrane potential and the action potential. These terms will be discussed in more detail throughout this section. The word potential means “having electrical charge.” Thus, when we talk about the potential that a cell membrane has because it has separated ions, we refer to it as the resting membrane potential. Later, we will talk about the membrane when it utilizes its potential, and we will call it the action potential. The resting membrane potential is due to specific ions, mainly potassium, and their tendency to diffuse down concentration gradients until opposed by electrical forces of opposite, but similar, magnitude.
To understand the resting membrane potential it is important to recognize that positively charged ions are attracted to negatively charged ions because of their valence charge, a resultant effect of an ion in a solution. It is also important to understand that in bulk solution, the number of positive and negative charges are always equal. The interaction of an ion with water is defined using a dimensionless (a measurement without units) value called the dielectric constant. When compared to the interior of the phospholipid bilayer membrane, the dielectric constant of water is approximately 40 times greater. Thus, for an ion, for example, Na+, to dissolve in the bilayer as opposed to water, is essentially zero. This is a fancy way of saying that the Na+ ion, without the aid of a protein-mediated selectivity filter, will not be able to cross the bilayer. This dielectric constant and the ability of proteins to close their gates and stop ion movement, allow the Na-K ATPase pump to separate ions, which in turn results in the separation of charge across the membrane.
Since the pump moves 3 Na ions (3 positive charges) out of the cell in exchange for 2 K ions (2 positive charges) inside the cell, it is tempting to think that this imbalance in charge is what causes the observed negativity of the inside of the cell membrane compared to the outside. However, consider that when the Na-K pumps of a squid axon are inhibited (using the antagonistic drug ouabain), the inside of the membrane that usually rests at a negative -60mV, initially only changes by a value of 1.4mV. This suggests that the pump does not contribute that much to the overall negativity. So what causes the negative inside? It appears that cell membrane negative potentials depend more on the ionic concentration gradient that was established by the pump than the actual pump itself.
To simplify, let's try an analogy. The figure below represents an artificial system of two chambers (A and B) separated by a membrane. We will assume that the membrane is permeable to cations (positively charged ions), but not to anions (negatively charged ions). If we placed two different concentrations of a KCl solution into each chamber, say 0.1 M solution of KCl in chamber B and a 0.01 M solution of KCl in chamber A, what would happen?

Image Created at BYU-Idaho by JH, 2013.
Above is an artificial container of water with a membrane in the center that is permeable only to cations. The membrane has just been placed in this figure, and no ions have moved yet.
Since the membrane is only permeable to cations, K+ will begin to diffuse from chamber B to chamber A, which is less concentrated (see figure below).

Image Created at BYU-I by JH, 2013.
K+ moves down its concentration gradient from high to low. When will the diffusion of K+ stop? You might be tempted to say, “When the two concentrations are equal, that is, when K+ on side B reaches the same concentration of K+ on side A.” In the previous section about simple diffusion, you would have been correct! But in this section, we are dealing with charged solutes (ions), and they don’t behave the same as non–charged substances. The rules change when things are charged. You see, initially, no electrical difference will exist between the two chambers; however, since the membrane is not permeable to Cl-, side B will begin to accumulate negative charges because the positive charges are leaving. Stated another way, chamber A will begin to accumulate positive charges because the K+ cations have moved into this chamber (see figure below).

Image Created at BYU-I by JH, 2013.
Above is an artificial container of water with a membrane in the center that is permeable only to cations. Note that the cation K+ moves "down its concentration gradient" to Chamber A but does not reach a concentration equilibrium because the electrical gradient is "pulling” K+ back to Chamber B.
The more K+ that flows from side B to side A, the larger the charge difference will be, and eventually, this will result in an electrical force (electrical gradient) that becomes strong enough to oppose the diffusion of K+ across the membrane. The net flow of K+ will stop when the force of the electrical gradient, the attraction from the opposite Cl- charge, equals the force of the concentration gradient. We call this a state of equilibrium, even though the numbers of K+ on side B will still be higher than side A. Because of the opposite force applied by the lonely Cl- ions, the K+ ions will not be able to move to equal concentrations. When the two forces, the electrical gradient and the chemical gradient, equal each other (equilibrium) and the net movement is zero, we call the state resting and can refer to the two combined gradients as the electrochemical gradient. We have now successfully created a state of charge separation and an electrical potential because side B is now negatively charged compared to side A, and although the ions are still crossing, in this case, the K+ ion, the net movement across the membrane is actually zero.
It is zero because at steady-state equilibrium, for every K+ ion that crosses from B to A, driven by the concentration gradient, another K+ ion will move from A to B, driven by the electrical gradient. The electrical gradient can be determined mathematically using the Nernst potential (sometimes called the "Nernst Equation").
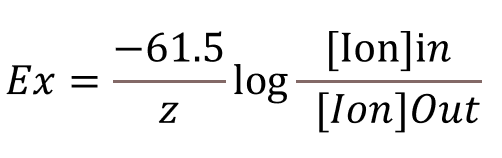
Variables Explained
Ex: The equilibrium potential for the ion (in millivolts, mV). This is the voltage at which there is no net movement of that particular ion across the membrane, because the electrical and chemical gradients balance each other out.
−61.5: This is a constant derived from the Nernst equation, where the values for the gas constant R, temperature T (set to 37°C), and Faraday’s constant F have been plugged in and simplified. The factor of -61.5 assumes body temperature and a conversion from natural log (ln) to base -10 log.
z: The valence (or charge) of the ion. For example:
- potassium (K+, z= +1)
- sodium (Na+, z= +1)
- calcium (Ca++, z=+2)
- chloride (Cl-, z= -1)
[Ion]in and [Ion]out: These are the concentrations of the ion inside and outside the cell, respectively.
This form of the equation calculates the membrane potential at which a specific ion is in equilibrium across the membrane. If the ion is positively charged and there is a higher concentration inside the cell, the equilibrium potential will be negative, indicating the inside of the cell is more negative than the outside for that ion. Conversely, if the ion is negatively charged, the sign of the potential will change accordingly.
The Nernst potential can predict the equilibrium potential of any ion as long as we know the concentration gradient of the ion. However, like most math equations, there are some built-in assumptions to make it all work, most of which do not actually apply in the “real world”. For instance, the Nernst equation assumes that the ion is completely permeable. This means that in the example above you could determine a Nernst potential for Cl-, but if you measured the actual resting membrane potential, it would look nothing like the calculated value because Cl- is not permeable in this system. Still, the equation is useful when applied to closed systems and when the assumptions are met.