3.17 Wanna Date?

Dr. Dan Moore and Dr. Brian Tonks, Geology and Physics Departments, BYU-Idaho

 What more can we require? Nothing but time.— James Hutton

Learning Objectives:

• Understand and be able to identify each of the following: element, isotope, radioactive, radioactive isotope, stable isotope, parent isotope, daughter isotope, probability of decay, and half-life.
• Understand why some isotopes are stable and others are radioactive and why some radioactive isotopes decay more quickly than others.
• Determine the number of half-lives that have passed given the proportion of parent and daughter atoms or a point on the radioactive decay curve. Also, determine the radiometric age of a specimen, given the number of half-lives that have passed.
• Know Earth’s age and why humanity’s confidence in this age is high.

Time is a simple four-letter word and permeates nearly every aspect of our existence. For example, it’s rare for us to be far from the clocks in cell phones, watches, and computers. Also, much of what we say includes references to time—“I’m going to …” or “I just …”. On the surface, time seems easy to understand. However, on closer inspection, we discover that time is much more expansive, deep, and strange than it seems.

Thinking critically about time requires considering foundational concepts like sequence, duration, rate, and cyclicity. Sequence relates to the ordering of events while duration describes the interval ‘length’ between events. Sequences allow us to describe cause-and-effect relationships and the temporal structure of nature. In addition, rates of processes indicate how quickly change occurs, and cyclicity describes recurring change. Scientists use these concepts to describe and measure time.

Human ability to accurately measure time has evolved. Aristotle believed time was unimportant, in part because humanity could not yet measure time accurately. During the Middle Ages, monks began using inaccurate mechanical clocks to regulate monastic life. Then, by the 1600s, accurate clocks allowed time to be included in Newton’s laws of motion and gravity. After Newton, humanity continued to develop ever more accurate timekeepers. Recently, humanity has used oscillations in cooled atoms to create an unfathomably accurate clock, which is so precise that it would ‘lose’ less than a second in 15 billion years.

Although modern clocks accurately measure time in the present, they cannot record unobserved periods in the past. As you know, natural clocks rely on rate-constant processes that record ‘ticks’ as time passes. Of these, radiometric dating is the most accurate, reliable, and widely applicable. It is also the least intuitive for those unfamiliar with the workings of atomic nuclei and the immensity of deep time. To help you understand isotopic dating, we explore the nature, functioning, and reliability of radioactive decay below.

The Nature of Radioactive Decay

Elements are atoms with specific numbers of protons, and isotopes are elements with specific numbers of neutrons. Stars form atomic nuclei with many combinations of protons and neutrons. Some of the isotopes made by stars are stable, others are unstable. When unstable or radioactive isotopes decay, they produce radiation.

The element carbon illustrates these ideas. All carbon atoms have 6 protons. Carbon consists of one radioactive isotope known as carbon-14 (which contains 8 neutrons) and two stable isotopes (known as carbon-12 and -13, containing 6 and 7 neutrons respectively). Carbon-14 is radioactive because a nucleus containing 6 protons and 8 neutrons is unstable. This instability ensures that carbon-14 eventually splits apart.

Radioactivity is an observational reality that results when radioactive parent isotopes spontaneously break down (decay) to form daughter isotopes. The rate of radioactive decay can be expressed as a decay probability or a half-life. The probability of decay describes how likely a nucleus will decay, and a half-life is the time required to produce equal proportions of parent and daughter atoms, from an initial state composed entirely of parent atoms. Highly unstable nuclei have high probabilities of decay and short half-lives (some far shorter than a second). In contrast, relatively stable radioactive isotopes have low probabilities of decay and long half-lives (some extending to billions of years).

To illustrate, carbon-14 has a high probability of decay and a short half-life (just 5730 years). In contrast, relatively stable potassium-40 has a low probability of decay and a long half-life (1.251 billion years). The half-life of radioactive isotopes determines their useful range as clocks. Many are useful between ~¹/_10,000 and ~10 half-lives. For example, C-14 can measure ages between ~500 ya and ~50 kya, and K-40 can date events older than ~15 kya.

Here’s the counterintuitive part about radioactivity: The same proportion of nuclei—not the same number of nuclei—always decay in the same period. Moreover, it is impossible to predict when any one radioactive atom will decay, but we can predict with tremendous accuracy the number of atoms that will decay in a given period. Um, what?

Fortunately for our physical intuition, radioactive decay follows the same probabilistic ‘law’ as dice, about which most humans have good intuition. Recall that for dice it is impossible to predict the number an individual die will display when rolled, but it is easy to predict the numbers of ‘ones’, ‘twos’, … that will appear after many rolls. This apparent paradox results from the probabilistic nature of dice. With each roll, the probability of a particular number appearing is always 1-in-6, or 16.67%. No matter how many times a die has been rolled, a new roll always has a 1-in-6 chance of producing a particular number. This fixed probability (¹/₆) is the reason it is easy to predict the proportion of ‘ones’, ‘twos’, … that will appear after many rolls. So, finding the number of ‘ones’ will appear in six million rolls, is easy: it’s ¹/₆^th of 6 million, or 1 million. Make sense?

Unlike dice, unstable atoms require no external agent. The constant motion of neutrons and protons inside the nucleus provide continuous opportunities for decay. What’s more, although rolling a million dice seems like a lot, there are huge numbers of atoms in even small amounts of matter. For example, a single die contains more than a trillion trillion atoms.

Despite these difference, in many important respects radioactive atoms behave just like rolled dice. For example, whether an atom decays in a particular moment has no effect on whether it will decay in the next moment. This happens because the probability of decay remains constant for each ‘roll of the atom’ (until, of course, it decays). Said another way, individual radioactive atoms do not have fixed lifetimes—they have fixed decay probabilities.

As you can now see, although the probabilistic character of dice and radioactive nuclei make them counterintuitive at first glance, once you understand how they work the apparent paradoxes evaporate.

How Radioactive Dating Works

Quite commonly, religious people looking for a way around Earth’s antiquity focus their scrutiny on radioactive dating. These individuals often reason that inconsistencies between young-Earth interpretations of written scripture and ancient-Earth witnesses of natural scripture result from variable decay rates or other problems with radioactive decay. Whether they realize it or not, those who discount the utility of radiometric dating place themselves in opposition to truth—to nature as it actually is. Why? Because abundant observations indicate that radioactive decay rates are constant and the ages recorded by radioactive decay are reliably accurate.

In addition to directly observing the radioactive decay of unstable isotopes with short half-lives, scientists have made numerous additional observations that fail to falsify the validity of radioactive clocks. For example, they have tested the constancy of decay rates by exposing radioactive atoms to physical conditions far more extreme than those found on Earth, by using multiple natural clocks to date the same event, and by making clever observations of naturally radioactive environments. These abundant tests clearly witness that half-lives are constant. Moreover, scientists have discovered that supernovae and naturally radioactive environments allow humanity to directly observe half-lives in the past.

Supernova 1987A (Figure 3.20) lies 168,000 lightyears from Earth, and radioactive decay produced much of the light it generated. Scientists were able to directly observe decay rates 168,000 years ago by studying the dimming of specific wavelengths of light from this supernova. Moreover, scientists were able to directly observe half-lives in a 1.7-billion-year-old nuclear ‘reactor’ on Earth (in Gabon, Africa), by studying the composition of reactor products. Importantly, these and similar observations were unable to falsify the constancy of radioactive decay rates.

Figure 3.20. Photo of a star (arrow) just and after it exploded to produce supernova 1987A. (NASA images)

Unrelentingly constant decay rates make radioactive isotopes excellent natural clocks. To understand how scientists use radioactive decay to measure the age of a geologic event, imagine a crystal growing as ancient magma cooled. As this crystal grew, it incorporated small quantities of radioactive parent atoms but no daughter atoms. Once solidified, the crystal became a kind of time capsule. As time passed, parent isotopes inside the crystal decayed to daughter isotopes according to the half-life of the radioactive isotope.

Imagine now that much later a geoscientist separates the crystal from the rock and measures the ratio of parent and daughter atoms in the crystal. These measurements indicate the number of half-lives that passed since the crystal formed, and this measurement gives the age of the crystal. The relationship (between radioactive parent isotopes, stable daughter isotopes, and half-life) used to calculate the age is illustrated in Figure 3.21.

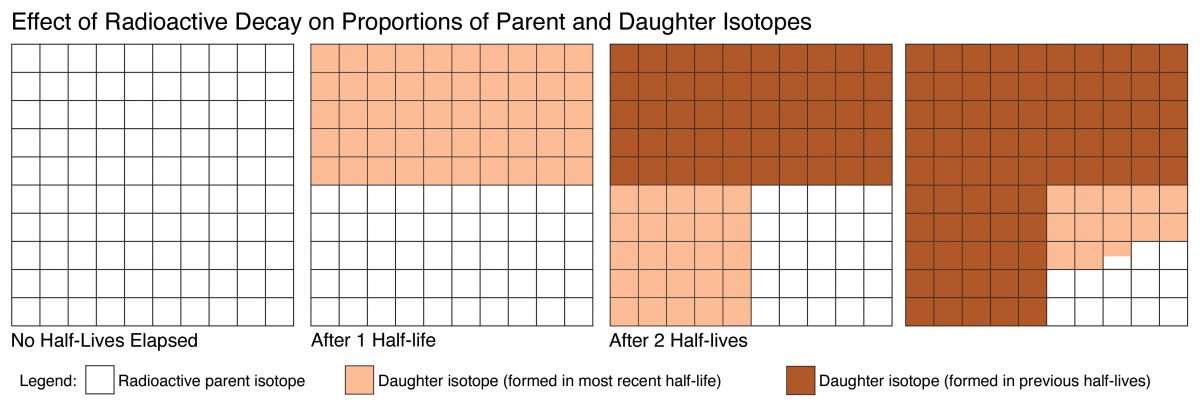
Figure 3.21. Illustration of radioactive decay through time. Note that half of the existing parent isotopes decay during each half-life.

(Radioactive decay, Author illustration, created as a work for hire by Eden Platt. Licensed as CC-BY- SA-3.0.)

Real measurements are more complex than those illustrated in Figure 3.21, but they follow the same pattern. For example, the number of half-lives recorded by real crystals is rarely whole numbers. More commonly, they are decimal fractions like 0.000041 or 6.7192. (Of course, such decimal fractions can also be expressed as fractions, percentages, or ratios.) Radioactive age determinations become more complex when growing crystals incorporate both parent and daughter atoms. The additional complexity requires different but equally valid approaches. (These are the so-called ‘direct-measurement of radiation’ and ‘isochron’ techniques.)

Despite these and other complications, scientists routinely measure formation ages for geologic materials with great accuracy and precision. For example, the first solids in our Solar System formed 4567.30 ± 0.16 Mya and the Little Cottonwood granite of Utah formed 29.75 ± 0.75 Mya. Notice that scientific ages include associated statistical uncertainty.

A set of mathematical equations describe the decay of radioactive parent atoms, the passage of half-lives, and the accumulation of stable daughter atoms. These quantitative relationships are represented graphically in Figure 3.22. Note that measurements of percent parent atoms remaining (or daughter atoms accumulated) determine the elapsed time (as measured in half-lives), and multiplying the ‘number of half-lives elapsed since formation’ times the half-life gives the formation age of the material.

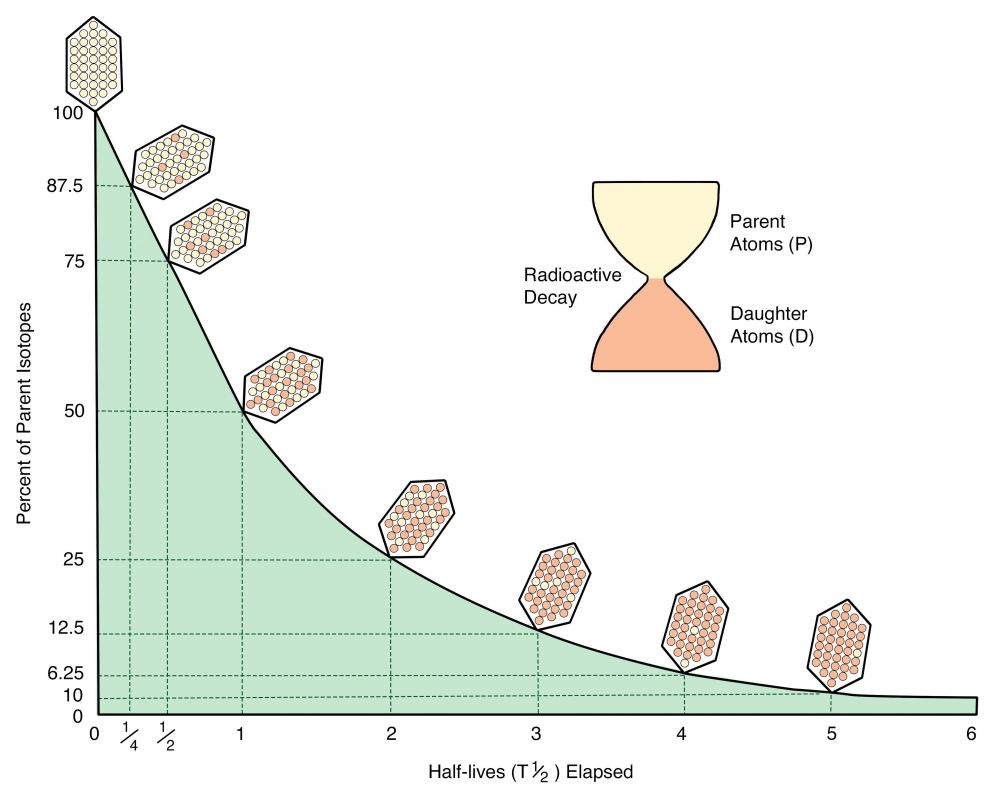
Figure 3.22. A plot of time (half-lives elapsed since formation) versus percent of parent isotope. The crystals illustrate the decay of parent atoms and the accumulation of daughter atoms.

(Radiometric decay, Author illustration, recolored as a work for hire by Eden Platt from USNOAA public domain image, https://bit.ly/38xSJV0. Licensed as CC-BY-SA-3.0.)

The Age of Earth

Observing that Earth is ancient is straightforward. For example, annual layers in trees, glacial lakes, and glaciers record ages up to ~60 kya. Likewise, the early molten Earth and fresh oceans required many millions of years to cool and become salty. Humanity used simple observations like these to discover Earth’s antiquity long before we learned how to use radioactive clocks to date past Earth events.

Today, modern instruments routinely measure radioactive ages with extreme precision. Uncertainties are typically less than 1%. Using radiometric dating, we can bracket Earth’s age by dating the materials from which Earth formed and the oldest known materials on Earth. Examples of these materials are shown in Figure 3.23. In this way, we know that Earth could not have formed before 4.57 Bya or after 4.4 Bya. What’s more, the ages of the oldest specimens from the Moon, Mars, and asteroids likewise witness that our solar system and the planets it contains formed during this period.

Figure 3.23. Photos of ancient rocks that help bracket Earth’s age. Left: A thumb-sized meteorite containing the first materials to solidify from the collapsing globule that formed our Solar System. These white irregularly-shaped grains are 4.567 Bya. Middle: A fist-sized specimen containing zircon crystals that formed 4.4 Bya in what is now western Australia. These crystals are Earth’s oldest known materials. Right: A hand-sized specimen of Earth’s oldest known rock body, which formed 4.01 Bya in what today is northwest Canada. 

(Ancient rocks, Author illustration, created as a work for hire by Eden Platt using author photographs. Licensed as CC-BY-SA-3.0.)

Helpful as they are, constraints provided by the oldest materials from Earth, Moon, Mars, and meteorites do not indicate Earth’s actual age. Fortunately, comparing the isotopic compositions of materials in Earth and primitive meteorites provides an answer. This important approach indicates that the materials that formed Earth separated from our proplyd by 4.54 Bya. Today, despite more than half a century of testing, humanity has been unable to falsify this ‘separation age’ for Earth.

In our experience, most who believe that Earth is young care little about Earth’s age. What most are trying to say when they dogmatically assert Earth’s youth is this: “God created Earth!”. These individuals often perceive that they must choose God or science, revealed or discovered truth, radiometric dating or written scripture. Impressively, most readily accept Earth’s antiquity once they understand the correct nature of and relationship between revealed and discovered truth.

In case it’s not already clear, the witness of natural scripture is unequivocal: Earth is ancient. It formed as part of our Solar System ~4.54 Bya.

For The Curious

Ancient Earth, Ancient Skies: The Age of Earth and its Cosmic Surroundings by Brent Dalrymple (2004, Stanford University Press).

The Man Who Found Time: James Hutton And The Discovery Of Earth's Antiquity by Jack Repcheck (2009, Basic Books).

The Dating Game: One Man's Search for the Age of the Earth by Cherry Lewis (2002, Cambridge University Press).