Plastic (High-Strain) Stress-Strain Behavior
4.5.1. Plastic Behavior and Definitions
Up to this point, the discussion of mechanical properties in solids has focused principally on situations of small strain (small movement) where behavior is elastic. The deviation from ideal elasticity in viscoelastic materials was addressed, but not the behavior of these materials at high strain (large deformations). In testing and in actual use high strains are often encountered. Therefore, the behavior of viscoelastic materials at large deformations is significant. A plot of stress versus strain over the entire range of strains is presented in Figure 4.9 for a typical polymer. It has some similarities to Figure 4.2 but differs in several important aspects.
The elastic region in the stress-strain curve of Figure 4.9 is the initial part of the curve, identified as linear. In this region the modulus is given by the Hooke's law relationship as shown in Equation (4.2). The point where the stress-strain curve begins to deviate from linearity is called the proportional limit. The importance of the proportional limit is mostly computational; that is, the modulus of the material must be measured before the proportional limit.
Slightly beyond the proportional limit is the yield point or the elastic limit. The yield point/elastic limit is the point at which the deformations of the material become partially nonrecoverable. In most metal and ceramic materials, the proportional limit and the yield point/elastic limit are the same. In most plastics, these two points are also quite close to each other and could be identical. However, in some plastics they are not the same and are, therefore, shown far apart in Figure 4.9 just to illustrate clearly that they are actually different points. In other words, in some plastics, the onset of nonlinearity may not result in permanent deformations. For instance, elastomeric materials can have highly recoverable properties (i.e., return completely to their original shape) but still be non-linear in their stress-strain behavior. A common elastic band has this behavior up to the point where it is stretched so far that it starts to break.
In structural materials, like metals and structural plastics, the yield point is important because it marks the upper limit of applied stress from which full recovery of shape occurs when the stress is removed. Imagine a coat hanger that deflects when a normal load (a coat) is placed on it and then, when the coat is removed, the hanger recovers (elastically) to its original shape. However, if an excessively heavy coat is put on it, the yield strength may be exceeded, in which case the hanger would be permanently deformed (although some elastic recovery would be seen, but not enough to regain the original shape). In nonstructural materials the yield point is less critical except when shape retention is important. If the stress is removed before the stress-strain curve reaches the yield point, full recovery will occur by either retracing the same path (full energy recovery) or by returning to the origin by a lower path (energy loss or hysteresis). Hysteresis is characteristic of viscoelastic materials.
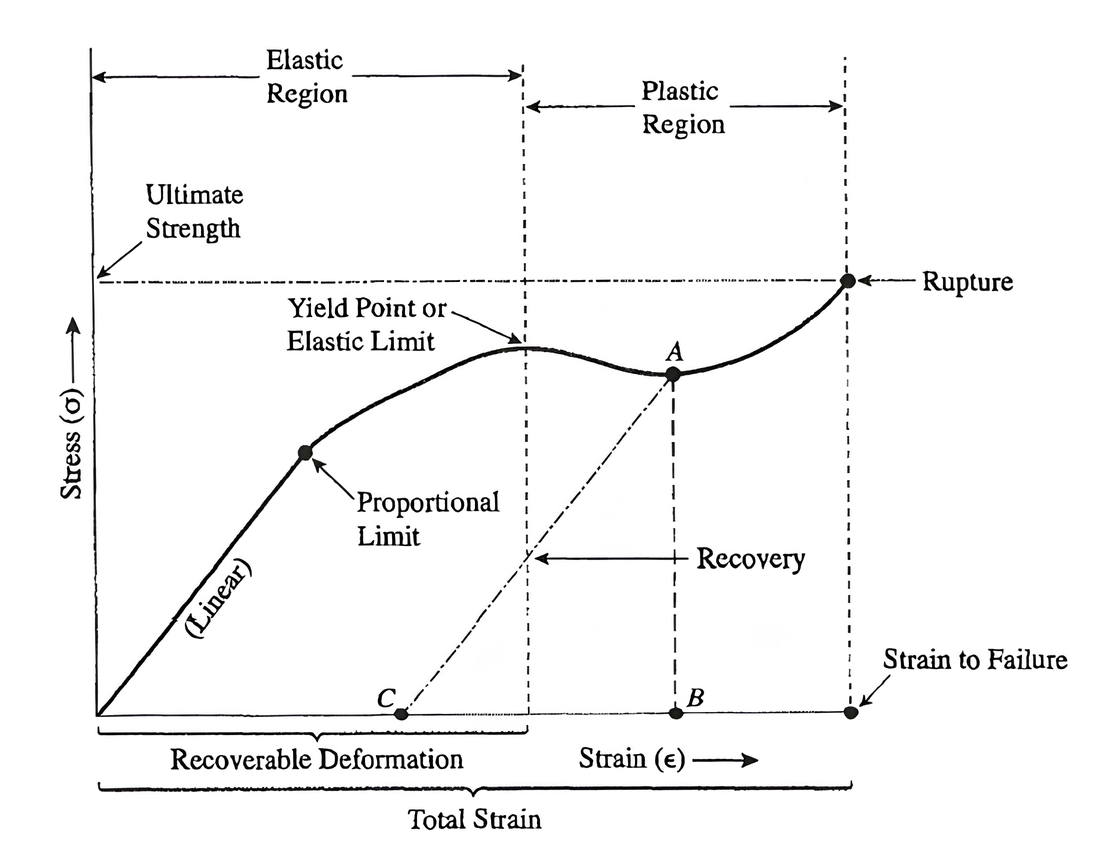
Figure 4.9 Stress-strain behavior over the entire strain range for a typical polymeric material.
Beyond the yield point, the material is permanently deformed. That is, even when the stress is removed, the material will not recover its original shape. The region beyond the yield point is called the plastic region. The nonrecovery of shape is indicated using point A in Figure 4.9 as the point where the stress is removed. Point A is in the plastic region, that is, beyond the yield point. The loading follows the curve past the yield point and finally reaches point A. The strain at point A is noted as point B. When the stress is removed, the material will recover part of its original shape and move from a strain of B to a strain of C. (The recovery actually follows the dotted line from A to C. The dotted line is parallel to the slope of the stress-strain curve in the elastic region unless hysteresis occurs, and then the recovery could be nonparallel.) The distance from the origin to point C is the amount of strain that is not recovered, or permanent deformation.
At some point on the normal stress-strain curve, a maximum stress level is reached. This highest stress that can be tolerated by the system is called the strength or the ultimate strength. (For tensile stresses, this value is called the ultimate tensile strength, or, by analogy, the ultimate flexural, compressive, or torsional strength, depending on the type of stress imposed.) If the stress is continued, the strain gets higher but the stress decreases because of the ability of the molecules to slide over each other. This produces movement (strain) in the polymeric structure but does not require increasing amounts of stress. Eventually, the maximum strain of the material is reached and rupture (breakage or failure) occurs. The strain value at rupture is called the strain to failure, that is, the accumulated strain or movement to the point of failure.
4.5.2. Interpretation of Plastic Behavior
The molecular interpretation (in polymers) of elastic and plastic behavior is that in the elastic region the strain results from recoverable movement stretching out of the twisted molecules in the amorphous regions and minor deformations in the crystalline regions. At the yield point, nonrecoverable movements begin that result in permanent deformation. Some of the most common are disentanglement of the molecules, slip of one molecule past another in a way that the slip could not be recovered, slip along a crystal plane, and formation of a crack. Further input of mechanical energy will lead to continued movement and increased energy in the molecule until the amount of energy in the molecule reaches the level of bond energies. At that point, further increases cause bond rupture and the sample breaks.
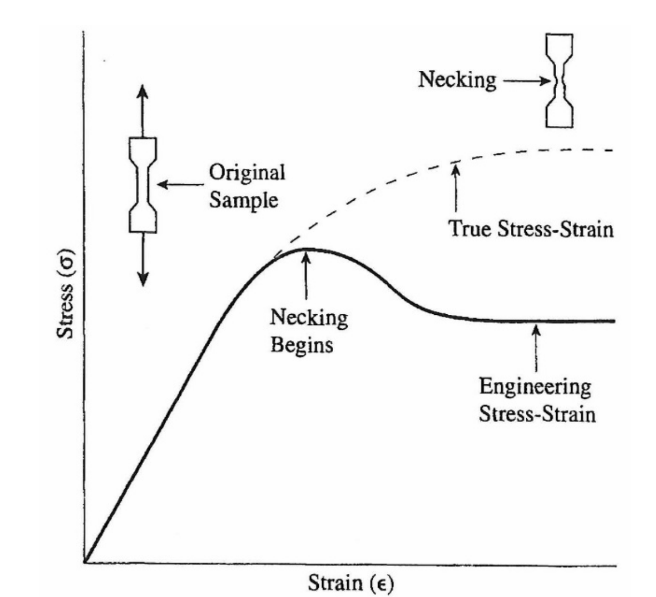
Figure 4.10 True and engineering stress-strain.
Behavior at the molecular level is illustrated in Figure 4.10 as the true stress-strain line. True stress-strain, as opposed to engineering stress-strain (the other line in Figure 4.10), is defined as the instantaneous value of the stress-strain curve (dσ/dϵ), rather than the change in strain divided by the original strain (Δϵ/ϵ0), which is the definition of engineering stress-strain. The true stress-strain is not used in common practice, but the situation depicted in Figure 4.10 illustrates its application. The true stress-strain curve shows the increasing resistance to the stress as the material deforms plastically. The engineering stress-strain, however, shows a reduction in the stress after the yield point. This reduction is a result of the thinning of the test sample. Because the sample thins (called necking), the force required to elongate the sample is greatly reduced and appears as a reduction in the stress-strain curve. In summary, the true stress-strain curve reflects what is actually happening at the molecular level a continuous increase in the stress while the engineering stress-strain curve reflects the necking of the sample and better indicates what a plastic part might do in actual use. Therefore, when the engineering strain-to-failure is reported, the value is often given as a ratio of the amount of deformation compared to the original length. In plastic materials, a related quantity, elongation, is even more commonly reported. It is simply the engineering strain-to-failure reported as a percentage of the original length of the sample.
4.5.3. Mechanical Model of Plastic Behavior
A model for the plastic deformation of viscoelastic materials can be built from classical mechanical elements, much as was done for the elastic and viscous cases. This model, shown in Figure 4.11, uses the spring and the dashpot elements and adds an element that represents a permanent deformation. The new element can be thought of as two pieces of sand paper, one stationary and the other pressed against the first. A minimum force is required to cause these two pieces of sandpaper to slide relative to each other, so some small movement can occur in the dashpot and spring without any movement in the sandpaper. If the minimum force that causes the sandpaper to slide is not exceeded, the movement of the system is reversible (returns to the original position when the force is relieved) and corresponds to elastic behavior. When the minimum force is exceeded, sliding of the sand paper will occur. This sliding is irreversible because the sandpaper will not slide back when the force is removed. This behavior corresponds to plastic behavior.
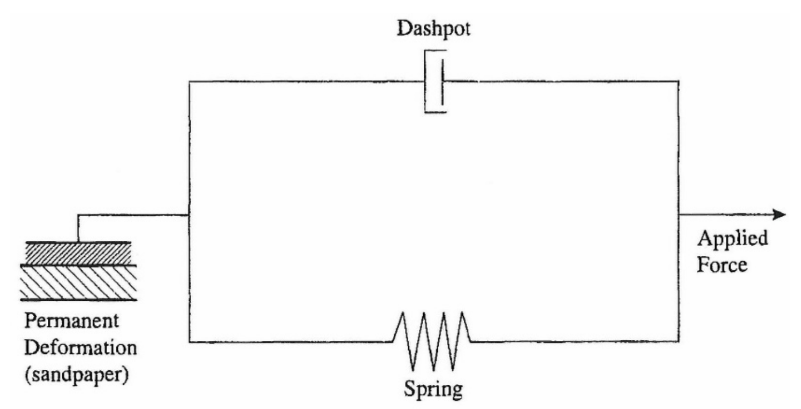
Figure 4.11 Mechanical model for plastic deformation of viscoelastic materials.
4.5.4. Tensile Forces
Tensile properties are determined using procedures such as those given in ASTM D 638. Normally, the sample is shaped so that the part will break be-tween the grips regions of the tensile test machine. The most common shape for plastic samples is a "dog-bone" shape, illustrated in Figure 4.12. The increased width of the sample in the gripping zones ensures that the sample will break within the failure zone.
The major plastic tensile properties determined by this test are tensile strength, tensile yield, tensile modulus, and elongation. Because of the viscoelastic nature of plastic materials, care should be taken to ensure that sample results to be com-pared are taken at the same rate of pull and at the same temperature, as these parameters can strongly affect the tensile results. The results of the tensile test are usually expressed as tensile strength (in psi or Pa), tensile modulus (in psi or Pa), and elongation (in inch/inch, mm/mm, or %).
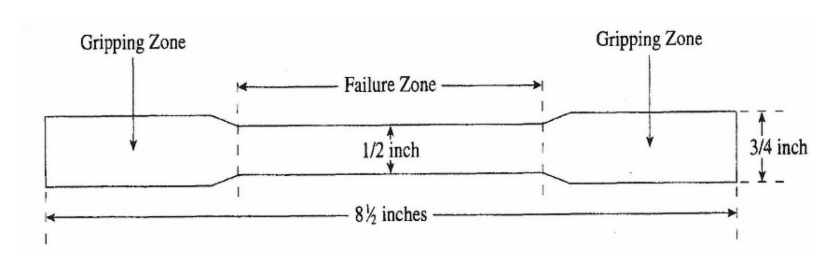
Figure 4.12 Typical tensile specimen shape (dog bone) for plastic samples.
4.5.5. Nontensile Forces
Mechanical behavior, elastic and plastic, has been described up to this point in terms of responses to a tensile force applied to the material. However, in Figure 4.1 several forces besides tensile forces were illustrated. All these forces are also important in plastic materials.
Compression Properties. Compressive force gives information about the strength and stiffness of a columnar sample that is supported vertically then pressed on its ends, as shown in Figure 4.13a. The equations and symbols for stress, strain, and modulus (σ, ϵ, E) developed for tensile force also apply to compressive force, but are termed compressive strength, compressive modulus, and so on. The compressive strength and modulus can be quite different from the tensile strength and modulus because of the difference in the ability of the polymer material to support a columnar load versus a pulling load. In general, for polymers compressive strengths and moduli are lower than tensile values.
Compression properties are measured following procedures such as those given in ASTM D 695. Compressive strength is not as significant in most plastics as are some of the other mechanical properties. Because of the low modulus of most plastics, the compression samples must be quite thick or be externally supported. The dependence of the test results on sample geometry has led the testing association to recommend that compression values be used for structural studies only if the test samples are the same shape as the parts to be in actual use.
For foam samples and other fairly thick plastic materials that are subject to forces on the flat surface, the compression test is very important but is usually run under quite different conditions than would be used with a rigid plastic sample. The compression tester for foam samples has a compression foot with a large diameter to limit the penetration and registers quite low loads. The compression test for foams is therefore somewhat different from other compression tests, as are many other tests associated with foam materials, such as open-cell content, compression set, tear-resistance, and the various cushioning tests described in Chapter 17. Test results are compression strength (psi or Pa), compression modulus (psi or Pa), and strain-to-failure (inch/inch, mm/mm, or%). This test is illustrated in Figure 4.13b. When the yield point is exceeded in compression, a permanent deformation or compression set occurs. This compression set is important in characterizing the behavior of flexible foams.
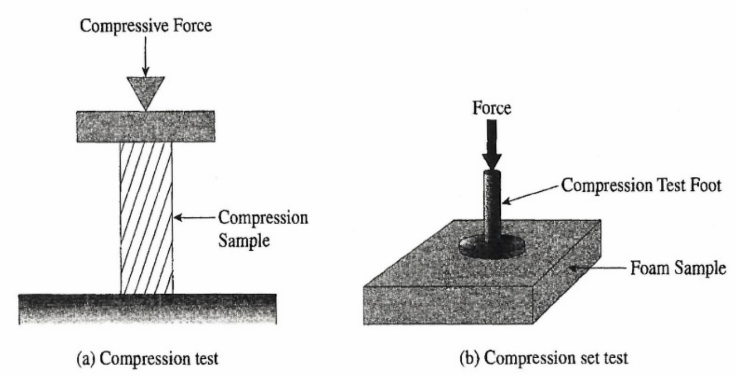
Figure 4.13 Compression test methods.
Flexural Properties. The symbols for flexural strength and modulus are the same as those for tension and compression forces. In fact, the bending forces used to determine flexural strength and modulus induce tension and compressive forces in the sample. It is not surprising, therefore, that flexural properties are often thought of as combinations of tension and compression.
The flexural properties are determined using procedures like those given in ASTM D 790. Many plastic parts are used in applications where flexural properties are important. For instance, plastic seating must have a minimum flexural strength and modulus or the seat will bend (sag) excessively or break. The flexural sample is a simple rectangular-shaped beam that is placed over two rests or supports and then loaded in the middle of the beam between the supports (see Figure 4.14). The beam is typically 1/s x ½ x 4 inches, although this size can vary for different materials. Results are given as flex strength (psi or Pa), flexural modulus (psi or Pa), and flexural elongation (inch/inch, mm/mm, or%). The flexural modulus is the most important flexural property for plastics.
Torsion and Shear Properties. The equations describing the torsion and the shear forces illustrated in Figure 4.1 do not use the same symbols as the tensile, compressive, and flexural forces, although the equations are of the same form. The stress-strain equation for torsion and for shear, analogous to Equation (4.1), is given in Equation (4.6):
where 7 is the shear stress, G is the shear modulus, and 'Y is the shear strain. The shear strain and its time derivative, the shear rate, were introduced when discussing the shears induced in viscous flow. Although the values for the shear strength, shear modulus, and other shear-related values may be quite different from the tensile-related values, the basic concepts regarding the microstructure origin of these parameters are generally analogous.
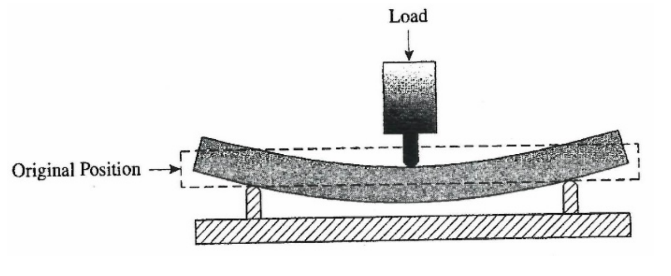
Figure 4.14 Flexural tensile and modulus test schematic.
Blushing. Plastic deformations from any type of stress will act first on the amorphous portions of the plastic. During the stretching and unfolding of the molecules in these areas, adjacent molecules can be brought into close alignment. This alignment can result in the formation of some crystallinity in that region, especially in simple molecules that align easily. This increased crystallinity can be noted by a change in the index of refraction of the polymer and the newly crystalline area taking on a cloudy appearance. This phenomenon, called blushing, is most common when a plastic is severely bent. The blushing appears at the outer edge of the bend where the tensile forces are the strongest and the molecules are stretched the most. The increased crystallinity at this site causes the local modulus of the material to increase. This phenomenon is, therefore, somewhat analogous to work hardening in metals. If the material is subjected to repeated bending at the same place, the material will eventually break because of the embrittlement from the higher crystallinity.